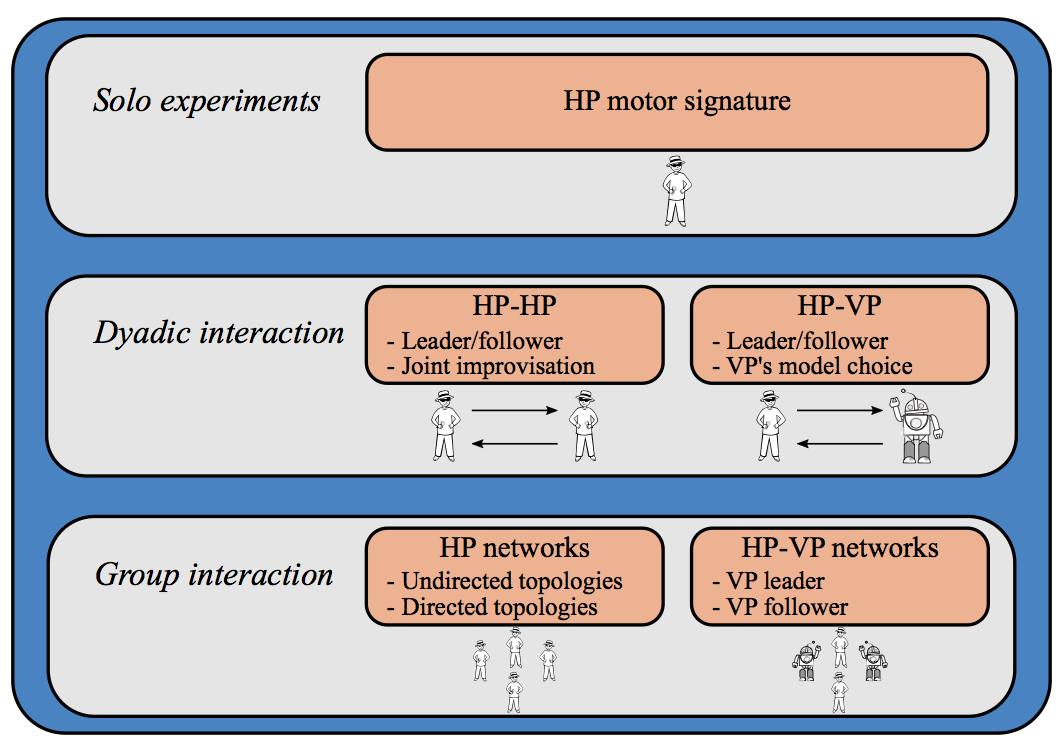
Let HP be an abbreviation of "human player" and VP of "virtual player".
Three different kinds of experiments can be performed:

1. Solo experiments - a HP performs spontaneous motion in isolation;
2. Dyadic interaction - both HP-HP and HP-VP trials can be performed;
3. Group interaction - both HP networks and mixed HP-VP networks can be implemented.

For more information on the VP’s mathematical model, see Cognitive architecture.

Hardware equipment

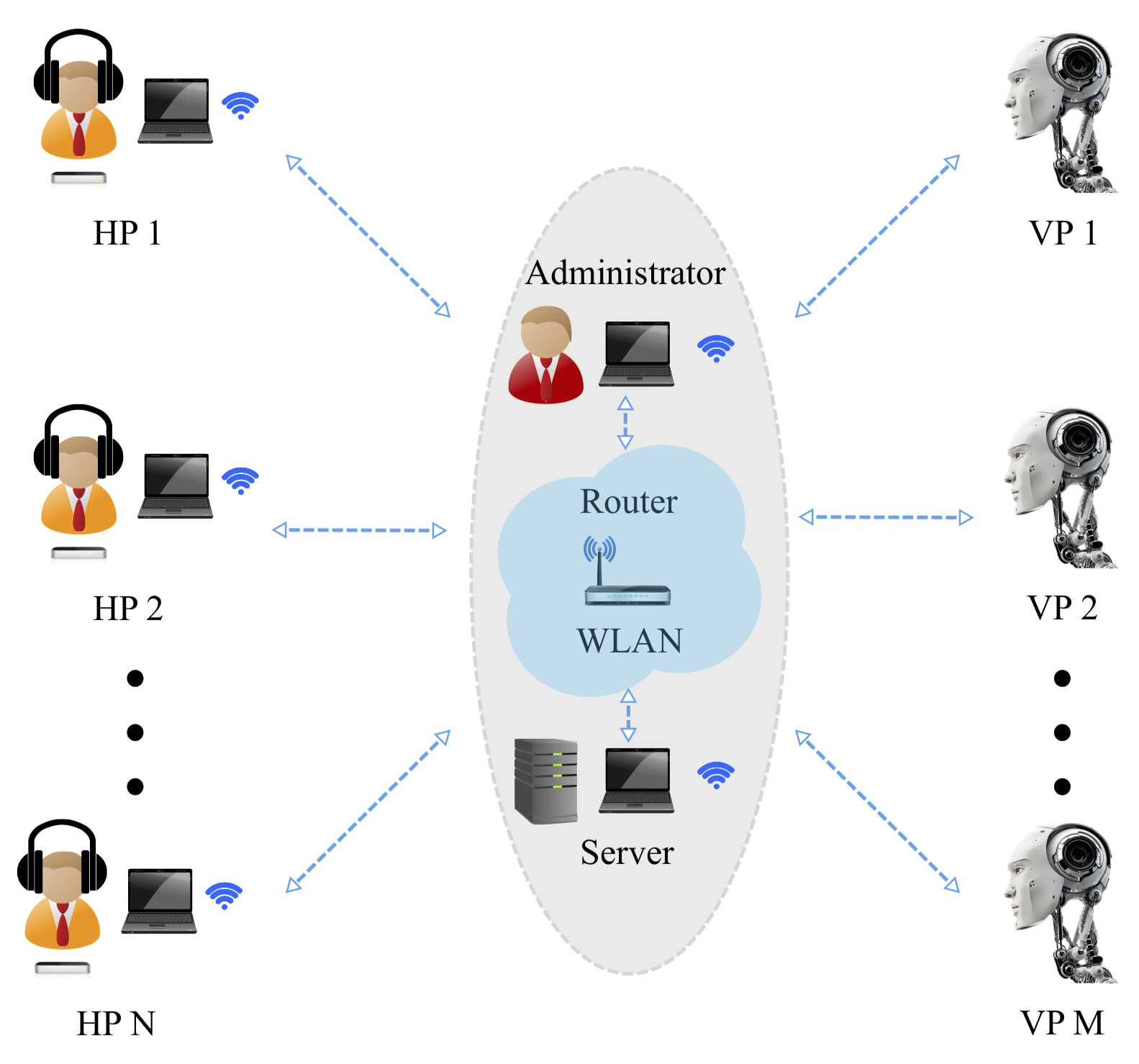
The hardware equipment consists of:

• N x Motion sensors. Each player waves the index finger over a Leap Motion controller (Leap Motion, Inc.) which captures its position trajectory over time [1]; alternatively, a mouse or trackpad can be used;
• N+1 x Personal computers. Each motion sensor is connected to a PC. Participants are able to see their motion and that of the others they are topologically connected with on their respective computer screens. One more computer is needed for server and administrator, while no more machines are needed to implement virtual agents;
• N x Headphones. Each player wears headphones through which white noise is transmitted;
• 1 x Router. It provides Wi-Fi signal in order to allow clients and server to be logged onto the same WLAN through TCP/IP protocol [2].

Software system

The software system, which is based on a client-server model [3], consists of:

• N x Player modules. These modules, respectively accessible by one human player each, provide a user-friendly interface through which participants can carry out the task of interest. In the case of Dyadic interaction, they also allow to set the trial duration and condition, as well as the virtual agent's mathematical model [4, 5];
• 1 x Administrator module. This module, accessible by the administrator only, carries out different duties through a user-friendly interface. In the case of Solo experiments, it allows to record the motor signature of a given human participant. In the case of Group interaction, it allows to set the topology of interaction among HPs and the duration of each trial, as well as the VP model in mixed HP-VP networks;
• 1 x Server module. It handles the communication among different machines and connects them onto the WLAN provided by the router. In the case of Solo experiments, it deals with the motor signature storage in an appropriate database.

Metrics employed

Let $x_k(t) \in \mathbb{R}\ \forall t \in [0,T]$ be the continuous time series representing the motion of the $k$-th agent, with $k \in [1,P]$, where $P$ is the total number of subjects and $T$ is the duration of the experiment. Let $x_k[t_i] \in \mathbb{R}$, with $k \in [1,P]$ and $ i \in [1,N_T]$, be the respective discrete time series of the $k$-th agent, obtained after sampling $x_k(t)$ at time instants $t_i$, where $N_T$ is the number of time steps of duration $\Delta T := \frac{T}{N_T}$, that is the sampling period. Let $\theta_k(t) \in [-\pi,\pi]$ be the phase of the $k$-th agent, which can be estimated by making use of the Hilbert transform of the signal $x_k(t)$.

When $P=2$ (Dyadic interaction), if we denote with $\phi_{d_{h,k}}(t):=\theta_h(t)-\theta_{k}(t)$ the relative phase between agents $h$ and $k$ at time $t$, it is possible to define the following parameter

$\rho_{d_{h,k}} := \left | \frac{1}{T} \int_{0}^{T} e^{ j \phi_{d_{h,k}}(t) } \ dt \right | \simeq \left | \frac{1}{N_T} \sum_{i=1}^{N_T} e^{ j \phi_{d_{h,k}}[t_i] } \right | \quad \in [0,1]$

as their dyadic synchronization index: the closer $\rho_{d_{h,k}}$ is to $1$, the lower the phase mismatch between agents $h$ and $k$ over the whole trial. Note that in a Leader-Follower condition, if $\phi_{d_{h,k}}$ is defined as the difference between the phase of the leader (player $h$) and that of the follower (player $k$), positive values indicate that the designated leader is successfully leading the interaction with the designated follower.

It is also possible to define the root mean square (RMS) of the normalized position error between two agents as

$\epsilon_{h,k} := \frac{1}{L} \sqrt{\frac{1}{T}\int_0^T \left( x_h(t)-x_k(t) \right)^2 \ dt} \simeq \frac{1}{L} \sqrt{\frac{1}{N_T}\sum_{i=1}^{N_T} \left( x_h[t_i]-x_k[t_i] \right)^2}$

where $L$ refers to the range of admissible position (e.g., the range of motion detected by the Leap Motion controller): the lower $\epsilon_{h,k}$ is, the lower the position mismatch between agents $h$ and $k$.

When $P>2$ (Group interaction), a further index can be used as measure of the overall coordination level among agents in the group. We first define the cluster phase or Kuramoto order parameter, both in its complex form $q'(t) \in \mathbb{C}$ and in its real form $q(t) \in [-\pi,\pi]$ as

$q'(t) := \frac{1}{P} \sum_{k=1}^{P} e^{ j \theta_k(t) }, \qquad q(t) := {\rm atan2} \left(\Im(q'(t)),\Re(q'(t)) \right) $

which can be regarded as the average phase of the group at time $t$. Denoting with $\phi_k(t) := \theta_k(t) - q(t)$ the relative phase between the $k$-th participant and the group phase at time $t$, we then define the relative phase between the $k$-th participant and the group averaged over the time interval $[0,T]$, both in its complex form $\bar{\phi}'_k \in \mathbb{C}$ and in its real form $\bar{\phi}_k \in [-\pi,\pi]$ as

$\bar{\phi}'_k := \frac{1}{T} \int_{0}^{T} e^{ j \phi_k(t) } \ dt \simeq \frac{1}{N_T} \sum_{i=1}^{N_T} e^{ j \phi_k[t_i] },\qquad \bar{\phi}_k := {\rm atan2} \left( \Im(\bar{\phi}'_k), \Re(\bar{\phi}'_k) \right)$

In order to quantify the synchronization level of the entire group at time $t$, we define the following parameter

$\rho_g(t) := \frac{1}{P} \left | \sum_{k=1}^{P} e^{ j \left( \phi_k(t)- \bar{\phi}_k \right) } \right | \quad \in [0,1]$

as the group synchronization: the closer $\rho_g(t)$ is to $1$, the smaller the average phase mismatch of the agents in the group at time $t$.

Its value can be averaged over the whole time interval $[0,T]$ in order to have an estimate of the mean synchronization level of the group during the total duration of the performance:

$\rho_g := \frac{1}{T} \int_{0}^{T} \rho_g(t) \ dt \simeq \frac{1}{N_T} \sum_{i=1}^{N_T} \rho_g[t_i] \quad \in [0,1]$